Python + ダイクストラ法 ( Dijkstra algorithm )で最短経路を求める

Python + ダイクストラ法 ( Dijkstra's algorithm )で最短経路を求めます．

問題
ネットワークの作成
ダイクストラ法の計算結果の保存
ダイクストラ法の計算結果の解釈
ダイクストラ法の実行
まとめ
参考サイト

# 問題

下記のネットワークでnode1からnode5までの最短経路を求めます．

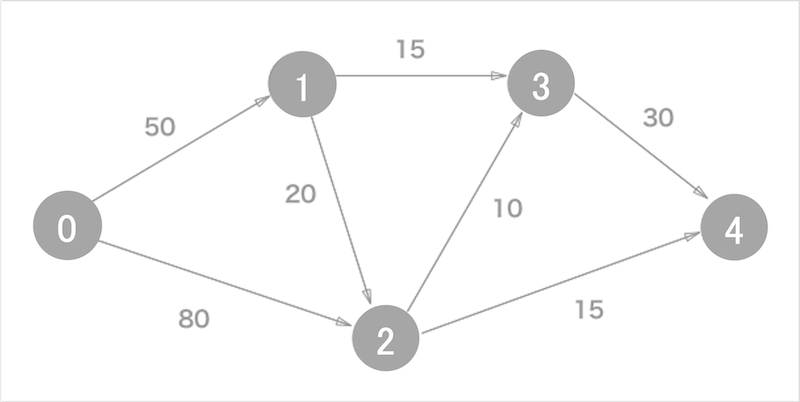
# ネットワークの作成

上画像より，正方行列でネットワーク情報を作成します

本稿では，nodeが5つあるので，5*5の行列で記述します．

行列内の要素は，今回は距離を入力する．交通容量を記入する場合や，台・kmも記入する場合もあります．

import math

# ネットワークを生成
# 初期のnode間の距離のリスト
route_list = [[0, 50, 80, 0, 0], #node-0
              [0, 0, 20, 15, 0 ] , #node-1
              [0, 0, 0, 10, 15], 
              [0, 0, 0, 0, 30], 
              [0, 0, 0, 0, 0]]

# nodeの数
node_num = len(route_list)

# ダイクストラ法の計算結果の保存

ダイクストラ法では，全経路を探索し最短距離の経路を後から選択するので，計算過程を保存する必要があります．

本コードでは，「未探索ノード・各nodeへの最短距離・各nodeをゴールとした場合，最終通過node」を格納するリストを作成します．

# 未探索ノード
unsearched_nodes = list(range(node_num))

# node-0から各nodeに到達する最短距離リスト
# node-0からstartは0とする
distance = [math.inf] * node_num
distance[0] = 0

# node-0から最短経路で各nodeに到達する場合，直前のnodeリスト
previous_nodes = [-1] * node_num

上記のコードだけではイメージがつきづらいので，先に上記の変数の最終結果を出力します．

# unsearched_nodesの最終結果
print('未探索ノードを下記に示す')
print([])
print("="*40)

# distanceの最終結果
distance_out = [0, 50, 70, 65, 85]
print('各nodeにおける，node-0からの最短経路')
for i in range(len(distance_out)):
    print(f"node-0からnode-{i + 1}までの最短距離 = {distance_out[i]}")
print("="*40)

# previous_nodesの最終結果
previous_nodes_out = [-1, 0, 1, 1, 2]
print('node-0から最短経路で各nodeに到達する場合の手前のnode')
for i in range(len(previous_nodes_out)):
    print(f"node-{i + 1}へ到達する手前のnode = {previous_nodes_out[i] + 1}")
    
# 出力
# 未探索ノードを下記に示す
# []
# ========================================
# 各nodeにおける，node-0からの最短経路
# node-0からnode-1までの最短距離 = 0
# node-0からnode-2までの最短距離 = 50
# node-0からnode-3までの最短距離 = 70
# node-0からnode-4までの最短距離 = 65
# node-0からnode-5までの最短距離 = 85
# ========================================
# node-0から最短経路で各nodeに到達する場合の手前のnode
# node-1へ到達する手前のnode = 0
# node-2へ到達する手前のnode = 1
# node-3へ到達する手前のnode = 2
# node-4へ到達する手前のnode = 2
# node-5へ到達する手前のnode = 3

下画像と各print文を見比べてください．

# ダイクストラ法の計算結果の解釈

ダイクストラ法の計算結果の解釈は，下記の通りです．

ダイクストラ法の計算過程 from hirasuYearEnd

# ダイクストラ法の実行

下記のコードでダイクストラ法による最短経路探索を実施します．

import time
start_time = time.perf_counter()

# 未探索ノード
unsearched_nodes = list(range(node_num))

# node-0から各nodeに到達する最短距離リスト
# node-0からstartは0とする
distance = [math.inf] * node_num
distance[0] = 0

# node-0から最短経路で各nodeに到達する場合，直前のnodeリスト
previous_nodes = [-1] * node_num

# 任意の最短移動距離で到達できる未探索node
def get_unsearched_next_node(moving_distance, 
                                 node_distance_list, 
                                 unsearched_nodes):
    search_idx = 0
    while True:
        min_node = node_distance_list.index(moving_distance, search_idx)
        found = min_node in unsearched_nodes
        if found:
            return min_node
        else:
            search_idx = search_idx + 1

#未探索ノードがなくなるまで繰り返す
while(len(unsearched_nodes) != 0):
    # STEP *-1 START
    # 現状移動させることができる最小距離
    posible_min_distance = math.inf # 初期値=inf
    # 未探索のノード内で移動最小距離を探索
    for node_index in unsearched_nodes:
        # より短い経路が見つかれば更新
        if posible_min_distance > distance[node_index]: 
            posible_min_distance = distance[node_index]
    
    # 移動最小距離で到達できる未探索のnodeを出力
    next_node = get_unsearched_next_node(posible_min_distance, 
                                         distance, 
                                         unsearched_nodes)
    # STEP *-1 END
    
    # STEP *-2 START
    # 到達できるnodeを未探索リストから除去
    unsearched_nodes.remove(next_node)

    # 到達できるnodeからのリンク(距離)を抽出
    next_node_link = route_list[next_node]
    # STEP *-2 END
    
    # STEP *-3 START
    for idx, link_dis in enumerate(next_node_link):
        # route_dis == 0は繋がっていないをことを示す
        if link_dis != 0:
            # ここでは各nodeへの最短距離を更新
            if distance[idx] > (distance[next_node] + link_dis):
                distance[idx] = distance[next_node] + link_dis # 過去に設定されたdistanceよりも小さい場合はdistanceを更新
                previous_nodes[idx] =  next_node #　ひとつ前に到達するノードのリストも更新
    # STEP *-3 END
    
execution_time = time.perf_counter() - start_time
print(execution_time)

# 実行時間
# 0.002838199958205223

下記のコードで結果を表示します．

print("-----経路-----")
previous_node = node_num - 1
while previous_node != -1:
    if previous_node !=0:
        print(str(previous_node) + " <- ", end='')
        # 最初に goal地点の'5 <- 'が出力
    else:
        print(str(previous_node))
    previous_node = previous_nodes[previous_node]

print("-----距離-----")
print(distance[node_num - 1])

# 出力
# -----経路-----
# 4 <- 2 <- 1 <- 0
# -----距離-----
# 85